[ Saiba atribuir e manipular materiais  no AutoCAD 20002 ]   Conheça a ferramenta do software que possibilita a aplicação de materiais em projetos 3D com características fotorrealísticas.

Crie uma escada caracol em 3D
Fábio Adriano Ferreira de Almeida

Esta rotina utiliza recursos que auxiliam sua criação em 3D no AutoCAD

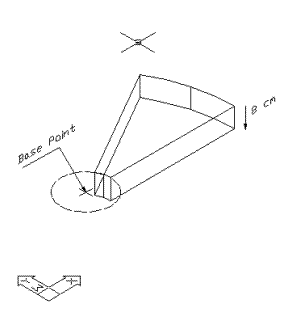
Escadas do tipo caracol são muito elegantes e bastante utilizadas em arquitetura. Essa é uma rotina simples que visa facilitar a criação de escadas e pode ser muito útil em seus projetos. Para iniciá-la, crie o diretório “C:\CADesign\Caracol3D”, digite a listagem abaixo em seu Visual Lisp ou bloco de notas e salve-a como “Caracol.3D.LSP”. Mas ainda não é tudo. Você ainda deve criar os blocos da coluna e degrau e salvá-los nesse diretório. As figuras abaixo mostram as medidas que foram utilizadas nesse exemplo. Você pode criar suas próprias medidas e salvá-las  como “Coluna” e “Degrau”. Veja figuras 1 e 2.
 

Fig. 1 – Exemplo de medidas dos blocos “Coluna” e “Degrau”		Fig. 2 – Detalhe do degrau

Para desenhar o degrau, defina um contorno e o transforme em polyline. Depois, aplique o comando Extrude para criar o degrau 3D. Note que o ponto de base é o centro do arco superior. No caso da coluna, dê um extrude com altura de 1 unidade. O sistema irá ajustar a altura da coluna automaticamente no momento da criação da escada.

Agora que criamos e salvamos a rotina Lisp e os blocos “Coluna” e “Degrau”, podemos carregar o programa com o comando APPLOAD. Um novo comando está disponível em seu AutoCAD: o comando Carac, que serve para criar escadas caracol. Informe a distância entrepisos e o sentido da escada. A rotina então desenha sua escada utilizando os blocos criados.

Fig. 3 – Escada Caracol 3D Renderizada
 

(defun c:carac (/ path h sentido degrau coluna pb ndegraus espelho
  angdif ang)
  (setvar "dispsilh" 1)
  (setvar "cmdecho" 0)
  (setq path "c:/CADesign/Caracol3D/")
  (setq degrau "degrau")
  (setq coluna "coluna")
  (setq h (getdist "\nDistância entre pisos: "))
  (if h
    (progn (initget "H A")
    (setq sentido (getkword "\nSentido H ou A: "))
    )
  )
  (cond
    (
     (and sentido (setq pb (getpoint "\nCentro da escada: ")))
     (command "insert" (strcat path coluna) pb "XYZ" 1 1 h 0.0)
     (setq sentido (if (= sentido "H") -1 1))
     (setq espelho 0.175)  ;valor max
     (setq ndegraus (fix+1 (/ h espelho)))
     (setq espelho (/ h ndegraus)) ;valor recalculado
     (setq angdif 30.0)
     (if (= sentido -1)
       (setq ang (- angdif))
       (setq ang 0.0)
     )
     (repeat ndegraus
       (setq pb (mapcar '+ pb (list 0 0 espelho)))
       (command "insert" (strcat path degrau) pb 1 1 ang)
       (setq ang (+ ang (* sentido angdif)))
     )
    )
  )
  (princ)
)

(defun fix+1 (n)
  (if (equal n (fix n))
    n
    (+ (fix n) 1)
  )
)
 

Rotina de LISP facilita a criação desses objetos e agiliza o trabalho

Fig. 4 – Mola 3D Renderizada
 

Mostraremos nesta coluna uma rotina em AutoLISP que desenha uma mola tridimensional, bastando para isso que o usuário informe os seis seguintes parâmetros:

- diâmetro Primitivo:  (ex. 4)
- altura da mola:        (ex. 7) (14)
- diâmetro do arame: (ex.1)
- número de voltas:    (ex.3) (6)
- densidade radial da malha 3D  (ex. 20)
- densidade longitudinal da malha 3D (ex. 80) (160)*

(*) Esses foram os novos parâmetros para a criação da ilustração

A rotina sempre desenha a mola na vertical, com o centro da primeira espira na origem do sistema de coordenadas global (WCS). Se você informar a altura igual a zero e número de voltas igual a 1, a rotina desenhará um torus (formato de uma câmara de pneu, por exemplo). Note que você também pode usar números fracionários para o número de voltas.
 

ROTINA

(defun mola (dp hp da nv dens_r dens_l / rp ra af ah p0 pf ang_l ang_r)
   (setq pi 3.14159265
         rp (/ dp 2.0)                                     ; raio primitivo
         ra (/ da 2.0)                                     ; raio do arame
         af (* 2 pi nv)                                     ; ângulo final
         ah (atan (/ hp (* rp af)))                     ; ângulo hélice
         p0 (list rp 0 0)                                  ; ponto inicial
         pf (list (* (cos af) rp) (* (sin af) rp) hp) ; ponto final
   )
   (setvar "cmdecho" 0)
   (princ "Aguarde...")
   (entmake
      (list
         (cons 0 "polyline")
         (cons 70 (+ 16 32))
         (cons 71 (+ 3 dens_l))
         (cons 72 dens_r)
      )
   )
   (repeat dens_r (cria_vertice p0))
   (foreach ang_l (list_ang dens_l nv T)
      (foreach ang_r (list_ang dens_r 1 nil)
         (cria_vertice (calc_ponto ang_r ang_l ra hp af)) 
     )
   )
   (repeat dens_r (cria_vertice pf))
   (entmake (list (cons 0 "seqend")))
   (command "vpoint" "1,-3,2.5")
   (setvar "cmdecho" 1)
   (princ "desenho concluido.")
   (princ)
)
 

(defun list_ang (nd nv tu / inc lst)    ; cria uma lista de ângulos
   (setq inc (/ (* 2 pi nv) nd)            ; nd = nº de divisões
         nd  (if tu nd (1- nd))              ; nv = nº de voltas
         lst (list (*  inc nd))                ; tu = tem último elemento
   )
   (repeat nd (setq nd (1- nd) lst (cons (* inc nd) lst)))
)
 

(defun calc_ponto (ang_r ang_l ra hp af / pn x y z)
  (setq pn (polar p0 ang_r ra)
        x  (* (cos ang_l) (car pn))
        y  (* (sin ang_l) (car pn))
        z  (+ (cadr pn) (/ (* hp ang_l) af))
        pn (list x y z)
  )
)
 

(defun cria_vertice (pt)
   (entmake
      (list
         (cons 0 "vertex")
         (cons 10 pt)
         (cons 70 64)
      )
   )
) 
 

(princ)

Fernando Palermo Simões é diretor da Lupa Computação Gráfica, desenvolvedora de aplicativos AutoLISP e digitalização 3D. E-mail: lupa@mandic.com.br

Maurijones de Albuquerque é analista de sistemas e professor de AutoCAD da ViewPoint, Assessoria e Implementações de Sistemas em Recife. Tel. (81) 3455-9720 - E-mail: maurijones@netscape.net